Data Structures
A data structure is a way of representing data in a program, and storing it in memory. There are many structures with their pros and cons, and uses cases. In these notes, we are going to go through some of them and look at how they function and when to use them.
Static Array
Arrays are a contiguous (non-breaking) space in memory with an index for each byte of memory.
Search
If the index of the target element is already known, then retrieving that item is a constant time operation, i.e. $O(1)$ However, if the index of the element is unknown, then we would have to walk the entire array, up until the index of the target element. Fetching from array therefor has $O(n)$ time complexity.
Insertion
To insert into an array, the value at the address is overwritten and the array size remains constant. Inserting into the middle of an array while maintaining data integrity, i.e. not overwriting, involves shifting all elements on position to the right, and inserting the element at the new blank spot. This means for a worst case non-overwriting insertion, we would have to shift $N$ elements for an array of length $N+1$ in order to insert at the beginning of the array. So the time complexity for this type of insertion is $O(n)$
Deletion
Deletion sets the value at the address to an agreed upon value meaning “Null”, i.e. zero 0. An array’s length cannot be decreased. If we want to ensure
the indices of elements match what is expected after a deletion, all elements to the right of the deletion have to be shifted one position to the left.
This is an $(n)$ in the worst case scenario.
Use Case
Arrays are basic data structures and can therefor be used in almost any situation, but they are mostly preferred where the items to be stored are few and is easy to know the index of the item you are looking for during an operation.
// static array in go
var items = [5]int{1,2,3,4,5}
Dynamic Array
A dynamic array is a type of array that appears to grow with the number of elements. They do not have a fixed length like a static array.
Search
A dynamic array is just a static array under the hood, so all search operations are the same as a static array.
Insertion
When a dynamic array is instantiated, it is created with slightly more space than is required. So if we create a dynamic array and store 4 elements in it, the underlying array can have 7 memory spaces instead of 4. This way if you were to append or push to the array, it will happen in constant time, because there is still space for 3 more elements in the array.
If we were to add 4 more elements, to the array, a new array with even more space, say 10, is created and all the previous elements are copied to the new array and the new elements are added to the new array instead. The process of copying over the elements can be assumed to be a constant time operation, and therefor ignored when estimating complexity. Therefor the insert operation with growing array is considered constant time complexity.
To insert in between elements, the shifting of all necessary elements has to happen, so the time complexity is $O(n)$
Deletion
To delete elements, pop operations are constant time and shift operations are linear time. Dynamic arrays seldom shrink, so the memory allocation remains the same after a deletion.
Use case
Dynamic arrays are the primary form of arrays used in many programming languages under the hood. Static arrays are useful when you know size of the data and all you are sure it will not grow. They provide better memory efficiency. Dynamic arrays are better for when the size of the data is unknown at time of creation. They take up more memory for the same number of elements, but they provide flexibility with size.
// dynamic array (slice) in go
var items = []int{1,2,3,4,5}
Linked Lists
Link lists are a type of node based data structure. A linked list is a collection of nodes that each contain a value, and a reference to another node.

When each node only has it’s value and a reference to one other node, the list is considered a Singly Linked List. As there is only a reference for the next node, we can only traverse the list in one direction and never in reverse.
In most cases, a doubly linked list is used. I.e. a list where the nodes contain the references to the next and previous node in the list.

Search
Since linked lists have no indices, and to get to one node, you need to go through all th preceding nodes that point to it, we have to traverse the list to find what we are looking for. In the worst case, we may have to go through N-1 nodes to find what we are looking for. This gives a complexity of $O(n)$.
Insertion
In order to insert a node $D$ into a doubly linked list $A \leftrightharpoons B \leftrightharpoons C$, we need to identify the 2 nodes $A$ and $B$ between which we will insert he new node $D$. We next pointer in $A$ to point to $D$ and set the previous pointer on $D$ to point $A$. We then change the previous pointer in $B$ to point to $D$ and set the next pointer in $D$ to $B$
At the end of all operations, the new list will become $A \leftrightharpoons D \leftrightharpoons B \leftrightharpoons C$.
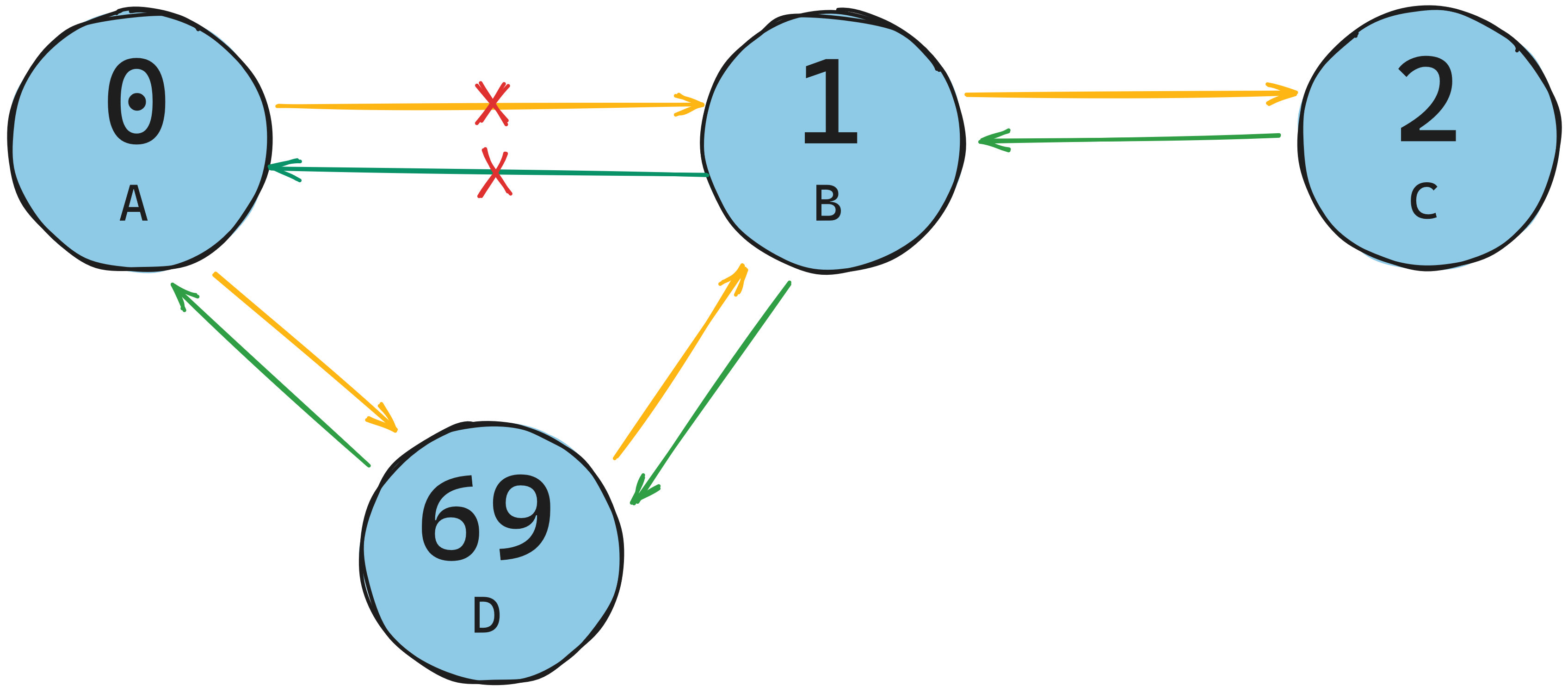
Setting the values for previous and next is a constant time operation, so $O(1)$ because we are setting 2 previous and 2 next pointer values, we will be perform 4 operations, i.e. $O(4)$, which according to the rules of Big-O, is considered $O(1)$. However, this is only true if we already know where we are inserting to. If we have to search for the insertion point, then we would have to do a linear search which would have a complexity of $O(n)$. Appending and prepending are a constant time operation, because we already know where the insertion point is.
Deletion
In order to delete a node, we can perform the insertion operation, but in reverse.
So if we want to delete $B$ from the array $A \leftrightharpoons D \leftrightharpoons B \leftrightharpoons C$ , we set next of $D$ to next of $B$ which is $C$ and remove the next of $B$. We then set previous of $C$ to previous of $C$ and remove previous of $B$. This will leave us with $A \leftrightharpoons D \leftrightharpoons C$. Since the operations are practically the same as insertion, the time complexity is still $O(1)$, but just like insertion, deletion complexity is subject if we have to find the deletion point first.
Use Case
A linked list, is a very good data structure to use for a queue. A queue is a first-in-first-out data structure, where items are appended at the tail and used as well as removed at the head. In queues, the head and tail nodes are the most important which means there is little to no need to find an node in the middle of the list. The following is an implementation of a singly-linked list as queue in Golang:
// Singly linked list implementation in form of a queue in go
package queue
type Node struct {
Value interface{}
Next *Node
}
type Queue struct {
Name string
Size int
head *Node
tail *Node
}
func (q *Queue) Enqueue(n *Node) {
if q.head == nil {
q.head = n
q.tail = n // if head is empty, then so is tail
} else {
q.tail.Next = n
}
q.tail = n
q.Size += 1
}
func (q *Queue) Deque() *Node {
if q.head == nil {
q.tail = nil
return nil
}
dequedNode := q.head // store the current head value before reassigning it
q.head = q.head.Next
q.Size -= 1
return dequedNode
}
func (q *Queue) PeekHead() *Node {
return q.head
}
func (q *Queue) PeekTail() *Node {
return q.tail
}
Stack
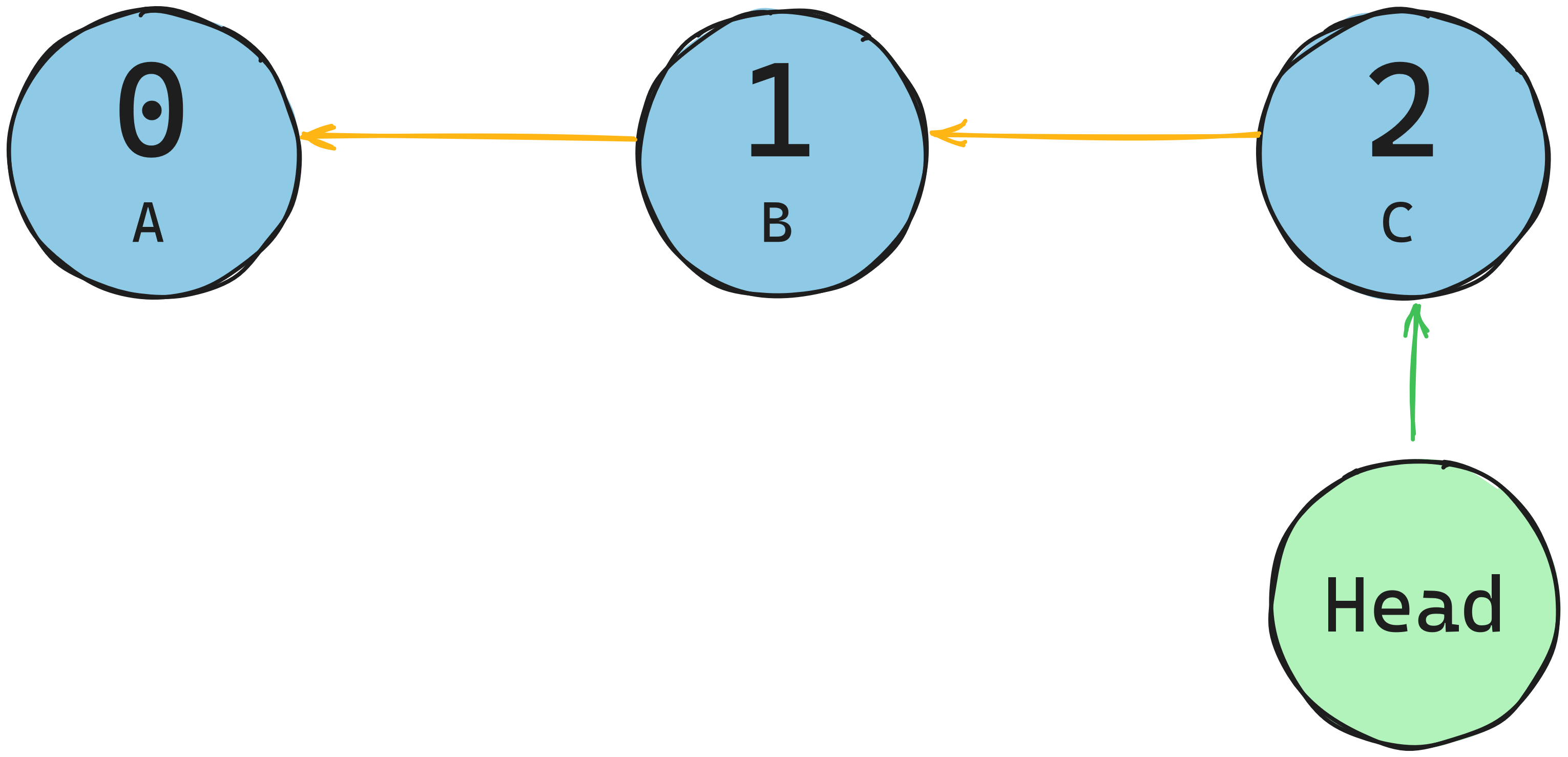
A stack is a the opposite of a singly-linked list (queue) where the head is at the tail and vice versa. Unlike the FIFO nature of a queue, a stack is First-In-Last-Out.
This means we are going to append to and remove from the head. In the diagram below, notice the pointers are going in the reverse direction compared to singly-linked lists
Search
Since stacks are FILO, we only need to get the node at the beginning of it. To know what is at the top of the stack, we can use a head to store a pointer to the first node. This is a constant time operation
Insert (push)
To insert a node, all we need to do set the new node’s previous pointer to the item pointed to by head, and then set the head pointer to the new node.
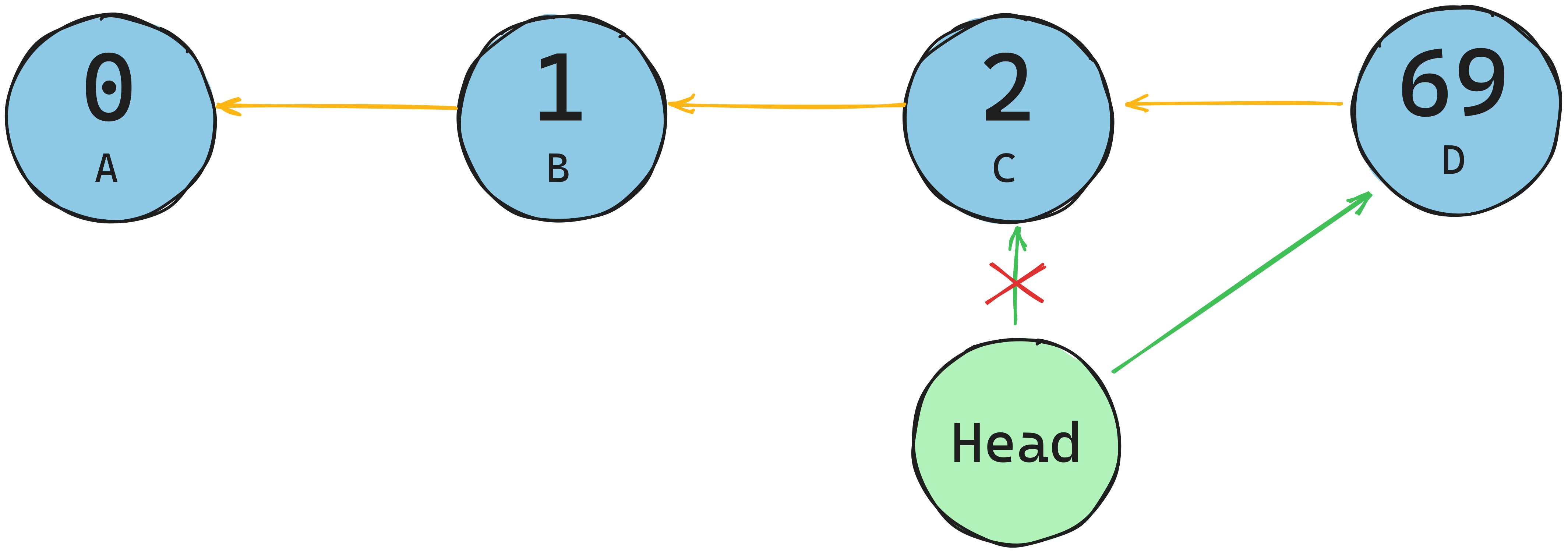
Deletion (pop)
To delete a node from a stack, we do the reverse of insertion: Take the node at the beginning of the stack and make the value it points to the new head, and remove it’s pointer.