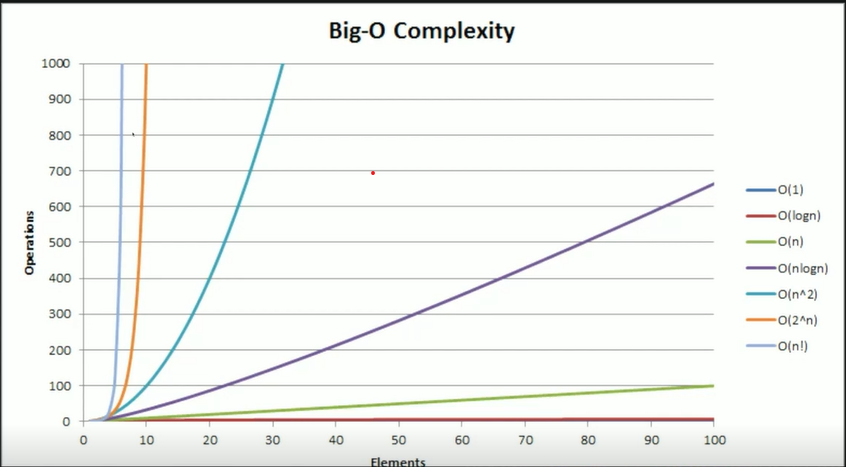
Big-O Complexity Notation
Big O complexity notation is used to give a general idea of the performance of an algorithm in terms of resources such as time or memory as the input grows larger. It is not a measure of true performance and is only a guide. The differences between the various algorithms are only seen on really large inputs.
The notation uses the syntax $O(v)$ where $v$ is an expression of complexity. d
General rules for Big-O notation are:
- Always ignore constants. This means $O(2n)$ and $O(\frac{1}{2}n)$ can be simplified to $O(n)$.
- Insignificant figures are ignored. So if you have $O(n^2\times\frac{n}{2})$ it is equivalent to $O(n^2)$ since $\frac{n}{2}$ is too small to have in impact
Examples of complexity for input size $n$ s are:
- $O(1)$
Indicates constant time where the execution time does not change with changing input size - $O(n)$
Indicates linear time where the execution time changes proportionally to the input size - $O(log \ n)$
Indicates that the execution time goes down logarithmically with input size. This is usually seen in algorithms where the iterative inputs are reduced to a smaller fraction of the previous input. - $O(n\ log \ n)$
Same as $O(log \ n)$ but the but by a magnitude $n$ - $O(n^k)$
Indicates exponential growth of magnitude $k$ - $O(n!)$ This is also an exponential grown but by the factorial on $n$ which is almost non-computable at certain values of $n$