SEARCH ALGORITHMS

Linear search goes over all elements and checks if it is the target element.
Since the search has to go through all elements in the worst case where there the values is not there, it has a complexity of $O(n)$.

// golang
package search

func Linear(items []int, target int) bool {
 for _, n := range items {
  if n == target {
   return true
  }
 }
 return false
}

Binary search is used to find items in an ordered list by iteratively halving the input. For each iteration we check the half that satisfies the bounding conditions of the search target and break it until we find the target or the target is not in the given input.

The bounds condition is usually $L \le T \lt U$ where $L=upper\ limit$ ,$\ T=target$ and $U=Upper\ limit$. The $U$ and $L$ are determined by the sorting order. So for example, if the items are sorted in alphabetical order, and a target $T$, the the first break will be $([A - M], [N - Z])$. Since $T$ is between $N$ and $Z$, we break the second list for the next search.
The index $M$ of the middle value is determined by:

$$ M = \left\lfloor \frac{(L + (U-L))}{2} \right\rfloor $$

The values for the lower and upper limits change depending on which of the 2 halves fit the conditions where we expect to find the target.

//golang
func Binary(items []int, target int) bool {
 upper := len(items)
 ascending := items[0] < items[upper-1] // incase we have a reversed array
 lower := 0
 middle := 0
 for {
  middle = lower + (upper-lower)/2
  if middle == len(items)-1 {
   return items[middle] == target
  }
  if middle == lower {
   return items[middle] == target
  }
  middleValue := items[middle]
  if middleValue == target {
   return true
  }
  if ascending {
   if target < middleValue {
    upper = middle
   } else if middleValue < target {
    lower = middle + 1
   }

  } else {
   if target < middleValue {
    lower = middle + 1
   } else {
    upper = middle
   }

  }

 }
}

With this implementation, we initialize upper bounds to be the length of the input and lower and middle to 0. The first condition to check is if we are at the end of the array. If array is sorted in ascending order and we are searching for a value that happens to be at the end, the search will tend to move towards the right and eventually get to the last element. We don’t want to search beyond that otherwise an index out of range will be raised at items[middle].

For every value of middle, we check if the value at the index matches our target and return true if it is. The next condition can be tricky but to understand, but I think it helps to only use the less than < or greater than > checks only instead of both. I prefer less than because it is easier to visualize the target either being on the left or on the right, and ‘discarding’ the rest.

If we have the first 10 values of the fibonacci sequence as our array: items = [0, 1, 1, 2, 5, 8, 13, 21, 34, 55]. We have this:

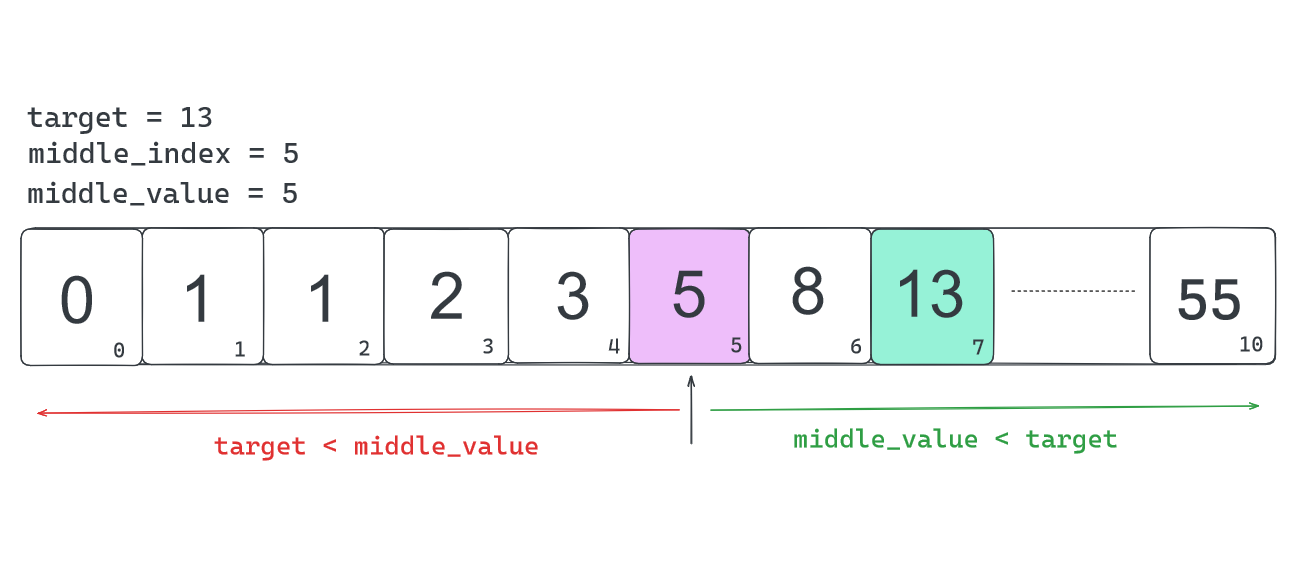
binary search visual
The middle value determines will become the new upper or lower depending on if it comes before or after target in the less than expression. i.e., if it comes after, then we discard all that is beyond it. If it comes before the target, then we discard all before it including itself.

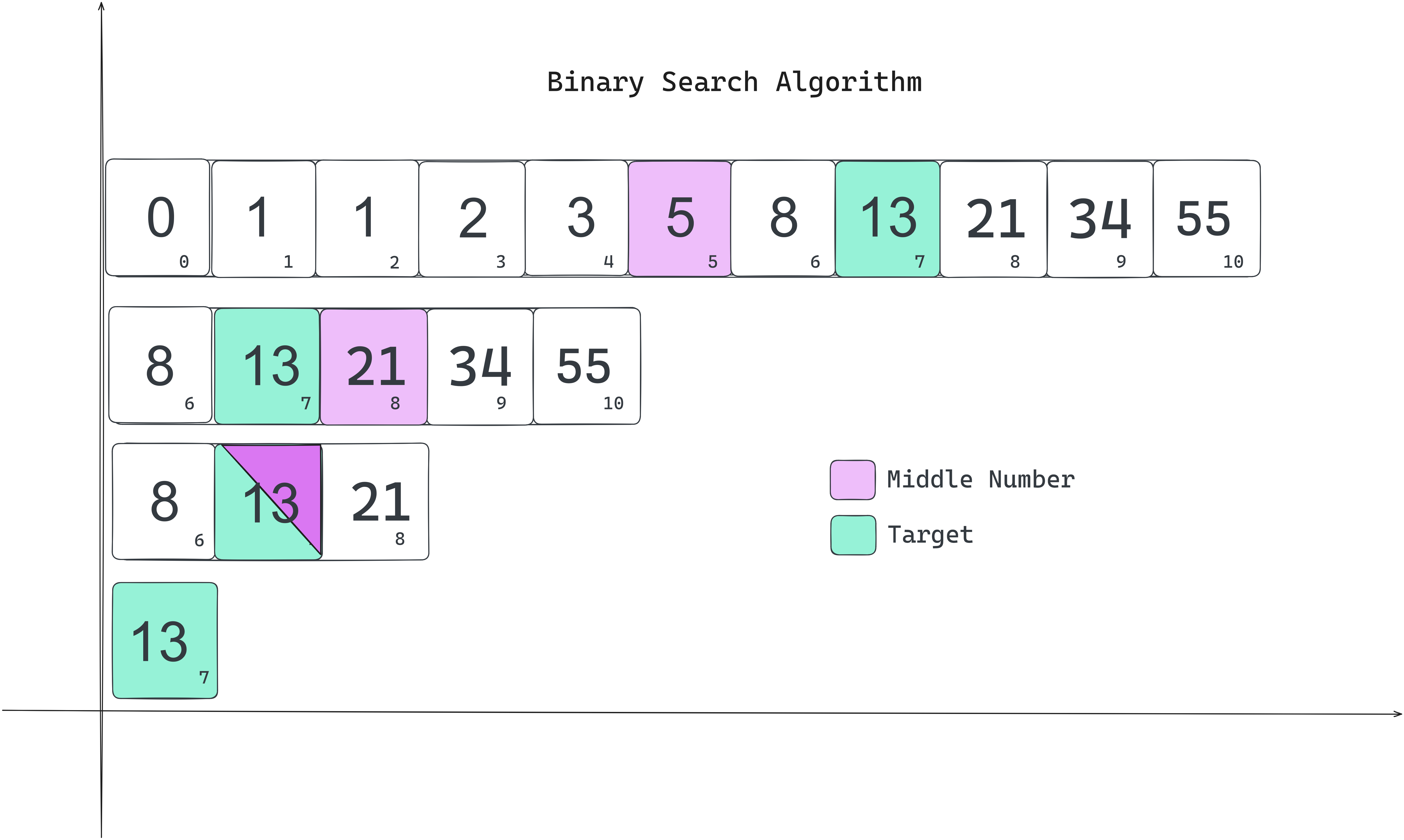If we complete the computation, for this list and do some clever ordering, you we can get the following graph Binary search graph AS you can see from the graph, the more items we have in the array, the the curve tends towards a flatness. For every iteration of the loop, the total search pool is halved, and so is the time that it would take to complete the search. Therefore, this algorithm has a complexity of $O(log\ n)$.

SORTING ALGORITHMS

A sorted array $X$ is mathematically defined as $X_i\lt X_{i+1}$ where $i$ is any index within list lower than the maximum i.e. $0 \le i \lt len(X)$

Bubble Sort

In order to do a bubble sort, we traverse the entire array and move compare each 2 consecutive values and check if the above condition is true. Swap their positions if they are not.

So if we have an array:

pi = [3, 1, 4, 1, 5]

we can sort them as below: 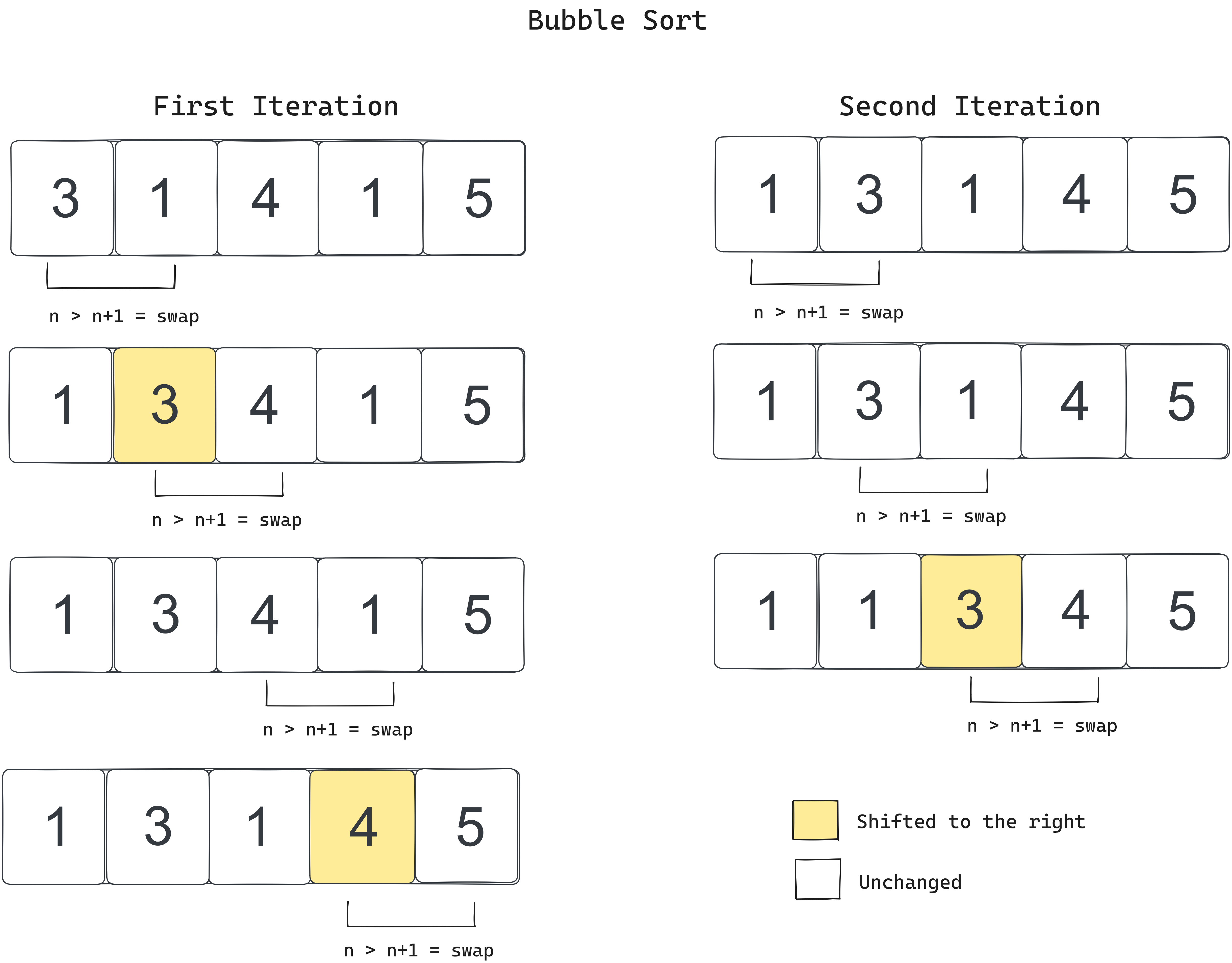bubble sort visual With each iteration, the largest values always get pushed to the end of the array, and thus, in the worst case, each iteration will doing 1 less check than the last iteration. Therefor the number of elements to to check for each iteration goes down with the following the following progression:

iter 1 = N
iter 2 = N-1
iter 3 = N-2
 .
 .
 .
iter Last = N-N+1

To get the total number of checks, we simply get a sum of all checks in the iterations. In our example, we have 5 elements, and the number of checks per iteration are:

5 + 4 + 3 + 2 + 1

The sum of all numbers in up to $K$:

$$ \Sigma_{n=1}^k = \frac{n(n + 1)}{2} = O\left(\frac{n(n + 1)}{2} \right) $$

According to the first rule of Big O, we ignore all constants, so the: $\frac{1}{2}$ can be ignored and we are left with:

$$ O(n^2 + n) $$

In the face of $n^2$, $\ + n$ is insignificant, so it can be dropped as well according to rule 2, leaving is with a complexity of $O(n^2)$

Here is an implementation of bubble sort in code:

// golang
package sort

func Bubble(items []int) []int {
last_item := len(items) - 1
 for range items{
  for i, v := range items {
   if i == last_item {
    break
   }
   if items[i] >= items[i+1] {
    items[i] = items[i+1]
    items[i+1] = v
   }
  }
  last_item -= 1
 }
 return items
}

Recursion

Recursion in programming calling a function within the same function. A function that calls itself is said to be recursive. Each recursion must have a base case where the the recursion will stop, otherwise it will go on ad infinitum or until compute resources are depleted.
A recursive function also needs a return value to pass back to itself for the next call. If the base case is reached, then the function will return a different value and not the function call of itself.